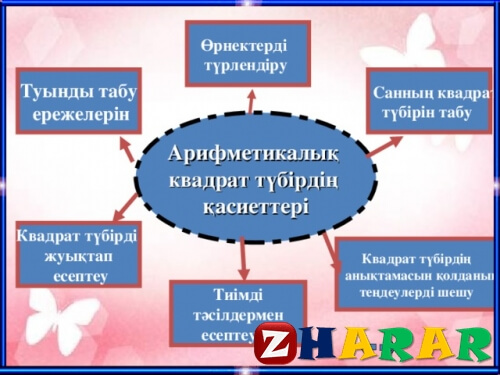
Арифметикалық квадрат түбірдің қасиеттері 3-сабақ (А-бөлімі) (Алгебра, 8 сынып, I тоқсан)

[quote] Пән: Алгебра
Ұзақ мерзімді жоспар бөлімі: Квадрат түбірлер және иррационал өрнектер
Сабақ тақырыбы: Арифметикалық квадрат түбірдің қасиеттері 3-сабақ (А-бөлімі)
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме): 8.1.2.1 арифметикалық квадрат түбірдің қасиеттерін қолдану
Сабақ мақсаттары: Оқушылар:
- арифметикалық квадрат түбірдің қасиеттерін квадрат түбірдің мәнін есептеуде және өрнектерді ықшамдауда қолдана алады;

1. Ұйымдастыру кезеңі: Оқушылармен сәлемдесу, түгелдеп, сынып тазалығы мен қажетті құрал-жабдықтарының дайындығын тексеру.
2. Үй тапсырмасын тексеру: Үйге берілген тапсырманы тексеру, оқушылар есебіндегі байқалған кемшіліктерді жою, оның пайда болу себептерін анықтау.

3. Математикалық софизм
Оқушыларға 4=5 болатынын дәлелдейтін математикалық софизмді көрсетіңіз.
16-36=25-45 екі жағына да 81/4 санын қосайық,
16-36+81/4=25-45+81/4 немесе
4^2-2∙4∙9/2+(9/2)^2=5^2-2∙5∙9/2+(9/2)^2
(4-9/2)^2=(5-9/2)^2 осыдан
4-9/2=5-9/2
4=5, яғни 2∙2=5.
Оқушылардан дәлелдеудің қателігін табу сұралады. Сонда олар 4-жолдағы (4-9/2)^2=(5-9/2)^2 теңдігінің екі жағынан да түбір қате табылғанын айтады. Бұл жерде теңдіктің екі жағынан да арифметикалық квадрат түбір алынғандықтан, анықтама бойынша түбірден шыққан сан теріс емес сан болуы керек, ал 4-9/20@-a,егер a0@b-a,егер a-b

Толық нұсқасын 30 секундтан кейін жүктей аласыз!!!

Қарап көріңіз 👇